Brief review on fix bed adsorber model:
The separation process can be carried out in a packed bed of sorbent particles. Our model is developed for cases in which intra-crystalline diffusion is the controlling resistance. Meso- and macroscopic diffusion resistances are neglected. Assuming plug flow, the concentration at any position and time can be obtained by solving a set of partial differential equations consisting of mass balances for the continuous and disperse phases.
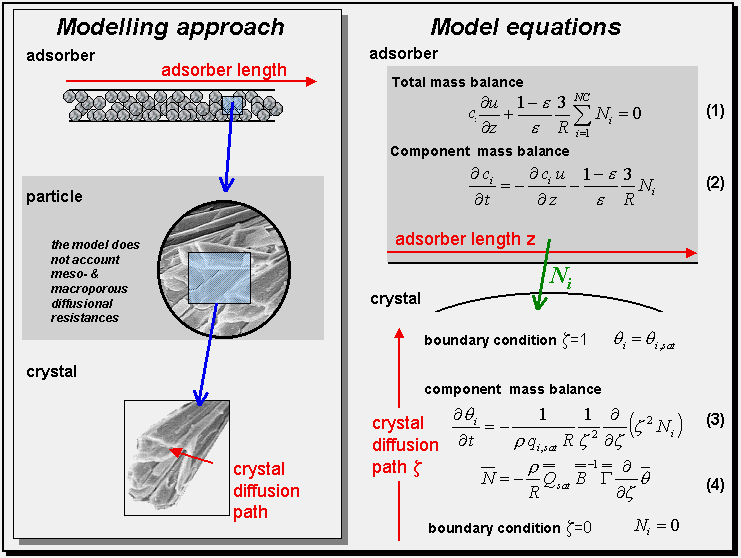
We assume an isothermal and isobaric reactor, in which a mixture of NC compounds is adsorbed under the presence of an inert compound. The inert compound does not adsorb and has no direct influence on the mixture isotherm. The concentration in the gaseous phase is calculated from the ideal gas law. Taking into account that the pressure and temperature are constant, we can determine the interstitial velocities along reactor from a quasi-stationary total mass balance, as shown in Eq (1).
The loadings along the crystal diffusion path are described by another partial differential equation; see Eq (3). We assume that the geometry of the crystal can be approximated by a sphere, where R is its radius, z is the dimensionless radial coordinate, qsat are the saturated molar loadings and q denotes the fractional loadings. The fluxes, N, are described by the Maxwell-Stefan equations; see Eq (4). The matrix B in Eq (4) describes the square matrix of inverse Maxwell-Stefan coefficients.
A detailed description of the model and further reading can be found in Krishna and Baur (2003).
Reactions: Optionally, the model also accounts for an arbitrary number of intra-crystal reactions, NR. In this case Eq (3) is extended by a reaction term.
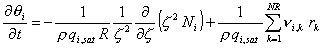
where rk is the rate expression for the kth reaction.
The rate expression for each reaction is based on a traditional Langmuir-Hinshelwood model, where the reactants, Ri, are absorbed on a free active site, S, and form the products, Pi. The products themselves will be desorbed and the occupied site will be freed.
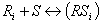
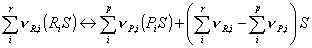
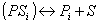
Note, the last term on the right hand side in the second equation denotes the number of sites, which are either released or occupied due to the reaction step. The adsorption, reaction and desorption step can be summarized in an overall balance:
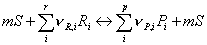
where m is the minimum number of free sites required for adsorption of the reactants and formation of the products
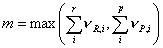
The number of free sites is proportional to the vacancy,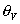 
, and so linked to the
isotherm. Clearly, the model described above pictures a very simple
situation where each species can only occupy a single site.
In order to derive an expression for the reaction rates we briefly focus on the thermodynamics of the adsorbed phase. We know that the Gibbs Free energy is at a minimum when the reaction is at chemical equilibrium. Analogous to aqueous reactions, we can show for the IAS theory that the chemical equilibrium constant equals the product of the activities:
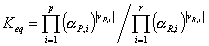
where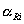 
are the
activities of the adsorbed reactants and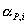 
of the products. The activities in an adsorbed
phase can be derived from the IAS theory and are given by:
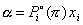
where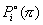 
is the equilibrium pressure for a pure component i and 
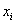the mole fraction in
the adsorbed phase. It is important to note that only in case of phase
equilibrium the activities in the adsorbed phase will equal the fugacity in
the continuous phase. In case of an ideal gas, for instance, this means
that the activities equal the partial pressures Pi.
The previous considerations motivate us to express the reaction rates in terms of activities and vacancy. Therefore, we apply a simple power law to the reaction balance. Assuming that the number of accessible free sites, S, is proportional to the vacancy, we obtain:
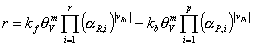
or
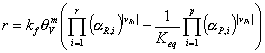
If (and only if) the adsorbed phase is in equilibrium with an ideal gas the equation simplifies to
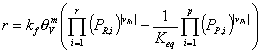
where PR,i and PP,i are the partial pressures in the gas phase. The expression above is consistent with the Langmuir-Hinshelwood reaction rate. In order to demonstrate this we derive a rate expression for an isomerization reaction:
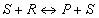
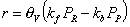
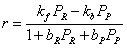
Choice of thermodynamic properties: Strictly speaking, the user can independently combine the methods for computing the isotherm, the thermodynamic correction factor and the square matrix of inverse Maxwell-Stefan coefficients. Below we list the implemented options: