Modelling issues of Zeolite based Separation Processes

Discretization scheme:

For the discretization of the partial differential equations, we applied a finite volume discretization scheme. This is illustrated in the figure below for the discretization of the crystal diffusion path in a fixed bed adsorber.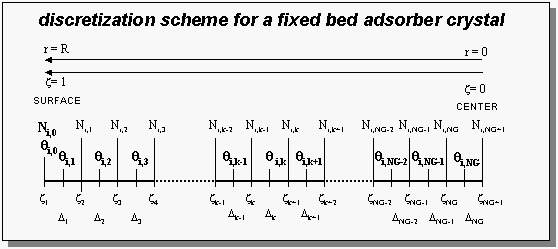

fixed bed adsorber crystal discretization

Quantities, such as fractional loadings (required to compute the fluxes at the boundary of a cell) are linearly interpolated from the values of the two neighboring cells. The spatial derivatives are approximated by central differencing. Generally speaking, we can approximate the derivative for a non-equidistant grid with cell width of D_k by:

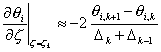
$derivative of the fractional loading within the crystal$

The derivative at the boundary of the pellet is derived by means of Taylor expansions:

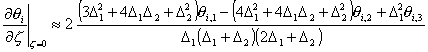
$derivative of the fractional loading at the outer boundary$

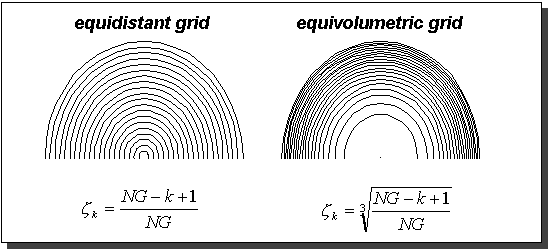
In case of the fixed bed adsorber, our program provides an equidistant or equivolumetric grid. The latter is preferably used for breakthrough simulations where steep gradients are generally expected at the outer boundary of the pellet. The figure below illustrates the difference of an equidistant and equivolumetric grid. The latter is much finer at the outer boundary of the sphere.

Calculation of the thermodynamic correction factor:

The thermodynamic correction factor is defined by means of the derivative of the partial pressures with regard to the fractional loading.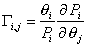

definition of thermodynamic
correction factor

The equations of the isotherm cannot commonly be explicitly expressed with respect to the partial pressures; hence the derivatives have to be determined numerically. This is a computationally very expensive procedure since it requires at least NC+1 iterative solutions for the isotherm. Our approach derives the thermodynamic correction factor from the derivatives of the isotherm residual vector. Therefore, this approach only requires a single iterative solution for the isotherm.

First, we numerically determine the partial pressures corresponding to the given fractional loadings from the isotherm. This solution results in a zero residual vector:

where the star denotes variables belonging to the computed solution.

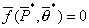
The total derivative of the residual with regard to the fractional loading is also zero (since the residual is zero for any desired solution). Hence, the derivative of the residual with regard to the fractional loadings can be expressed as:

We can obtain the thermodynamic correction factor for the previously numerically determined solution from the equation above and its definition:

Note, all derivatives of the residual vector can be obtained analytically. This allows implementing a highly efficient code for evaluating the thermodynamic correction factor matrix.

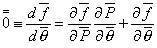
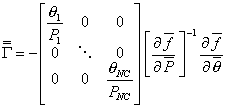
Sparse matrix DAE solver:

The resulting set of differential-algebraic equations (DAE) for our fixed bed adsorber problem is solved using BESIRK (Kooijman, 1995; Kooijman and Taylor, 1995), a sparse matrix DAE solver. BESIRK is a semi-implicit Runge-Kutta method originally developed by Michelsen (1976) and extended with an extrapolation scheme (Bulirsch and Stoer, 1966), improving the efficiency in solving the DAE problem. The evaluation of the sparse Jacobian is primarily based on analytical expressions.

Return to contents or next: sample runs.

Last update: Dec 01, 2002